1.学习总结

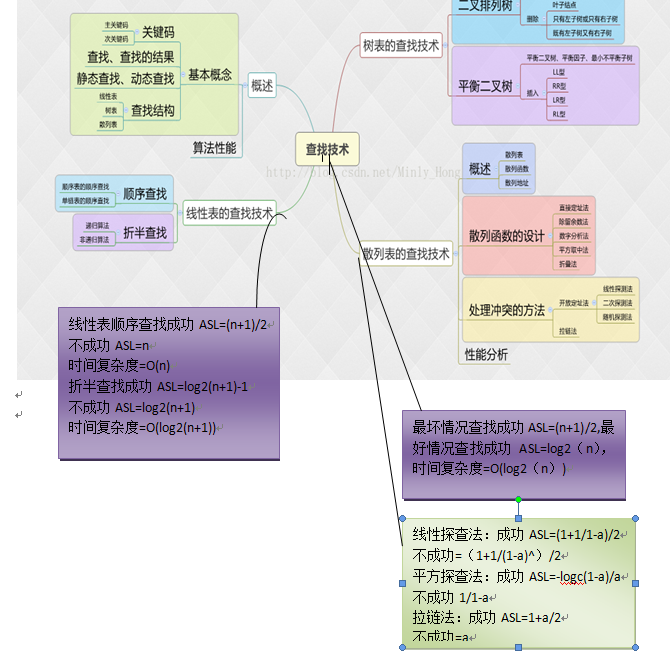
1.1查找思维导图

1.2查找学习体会

本章主要讲述各种查找技术，理解查找的基本概念，包括静态查找和动态查找，内查找和外查找以及平均查找长度的概念。然后有学习了线性表的顺序查找，折半查找，以及这些查找方法对应的ASL和时间复杂度。接着引入了树的概念，介绍了二叉排序树，AVL树，B-树，B+树以及他们的算法实现，查找效率。最后讲述散列表也就是哈希表的查找技术，以及解决“哈希冲突”的方法和其对应的ASL。在这一章的学习中，刚开始线性表学习起来还是很轻松的，但是讲到树的时候，会有些吃力，尤其是各种树的查找，插入，删除，以及他们的代码实现。代码不能靠看，要自己写才能记忆深刻，所以自己课下又在pta上写老师布置的作业，慢慢掌握了一些，但是还是不怎么熟悉。但是熟能生巧，只要勤加练习，我相信我可以自己独立完成。

2PTA实验作业

（1）2.1题目1：是否二叉搜索树

2.2 设计思路

只要判断其非空左子树的键值都小于其根节点的键值，其非空右子树的键值都大于其根节点的键值即可说明此树为二叉搜索树。显然这里要递归调用这个函数，先看根节点的左子树其键值是否小于根节点，小于的话，就看这个子树的左子树，以此类推，调用这个函数，右子树同样的方法。

2.3代码截图

2.4PTA提交列表说明

刚开始提交编译错误，是因为没有注意大小写一致，后来部分正确，没有考虑到只有根节点的情况和左右都为二叉搜索树但没能让其结果返回true.后来改正之后，还是没能完全正确，这个代码我是有定义了两个函数，分别用来求左子树上的最大值和右子树上的最小值。可能最后两个都满足情况的代码有点混乱，以至于实现不了。后来我就换了一个方法，只要把大化小，先比较根节点，根节点左子树，根节点右子树的键值，然后比较根节点左子树的左子树，右子树，这里要用递归算法来实现，同样，根节点右子树也是一样，这样代码量大大减少，而且思路很清晰，解决了之前遇到的问题。

（2）2.2题目2：二叉搜索树中的最近公共祖先

2.3设计思路

有两种情况：1.u,v不在树中；                    2.u,v在树中：<1>u,v都在左子树上；                                         <2>u,v都在右子树上；                                         <3>u,v一个在左子树上，一个在右子树上；                                         <4>u，v有一个在根上。

从树的根节点开始和两个节点作比较，如果当前节点的值比两个节点的值都大，则这两个节点的最近公共祖先节点一定在该节点的左子树中，则下一步遍历当前节点的左子树；

如果当前节点的值比两个节点的值都小，则这两个节点的最近公共祖先节点一定在该节点的右子树中，下一步遍历当前节点的右子树；这样直到找到第一个值是两个输入节点之间的值的节点，该节点就是两个节点的最近公共祖先节点。

2.4PTA提交列表说明

刚开始自己对这题也没有思路，只知道特殊情况，v,u有一个在根上，以及v,u分别位于左，右子树中，后来和同学讨论理清了思路，根据二叉搜索树的左子树<根节点<右子树的特征，先遍历树，若v,u都小于当前节点键值，那么其公共最近祖先一定在左子树中，若v,u都大于当前节点键值，那么其公共最近祖先一定在其右子树中

（3）2.3题目3：

航空公司VIP客户查询

设计思路：

建立一个不占多少内存但是又很巨量的指针数组

然后采用 身份证号处理 第6，10，14，16，17，18位 转换为哈希地址

然后将每个身份证号插入哈希链表（指针数组） 2.4 PTA提交列表说明

这个题目是问同学的，因为自己对哈希表方法还不很懂，虽然理解哈希表，哈希冲突，但是具体应用还是不怎么会，这个题目有听懂，是看着别人代码敲的，接下来会再接再厉

3.

3.1截图本周题目集的PTA最后排名

3.2我的总分

4.阅读代码

红黑树是一种近似平衡的二叉查找树，它能够确保任何一个节点的左右子树的高度差不会超过二者中较低那个的一陪。具体来说，红黑树是满足如下条件的二叉查找树（binary search tree）：

1. 每个节点要么是红色，要么是黑色。
2. 根节点必须是黑色
3. 红色节点不能连续（也即是，红色节点的孩子和父亲都不能是红色）。
4. 对于每个节点，从该点至null（树尾端）的任何路径，都含有相同个数的黑色节点。

在树的结构发生改变时（插入或者删除操作），往往会破坏上述条件3或条件4，需要通过调整使得查找树重新满足红黑树的条件。

左旋

左旋的过程是将x的右子树绕x逆时针旋转，使得x的右子树成为x的父亲，同时修改相关节点的引用。旋转之后，二叉查找树的属性仍然满足。

右旋

右旋的过程是将x的左子树绕x顺时针旋转，使得x的左子树成为x的父亲，同时修改相关节点的引用。旋转之后，二叉查找树的属性仍然满足

get()

get(Object key)方法根据指定的key值返回对应的value，该方法调用了getEntry(Object key)得到相应的entry，然后返回entry.value。因此getEntry()是算法的核心。算法思想是根据key的自然顺序（或者比较器顺序）对二叉查找树进行查找，直到找到满足k.compareTo(p.key) == 0的entry。

put()

put(K key, V value)方法是将指定的key, value对添加到map里。该方法首先会对map做一次查找，看是否包含该元组，如果已经包含则直接返回，查找过程类似于getEntry()方法；如果没有找到则会在红黑树中插入新的entry，如果插入之后破坏了红黑树的约束，还需要进行调整（旋转，改变某些节点的颜色）。

remove()

remove(Object key)的作用是删除key值对应的entry，该方法首先通过上文中提到的getEntry(Object key)方法找到key值对应的entry，然后调用deleteEntry(Entry<K,V> entry)删除对应的entry。由于删除操作会改变红黑树的结构，有可能破坏红黑树的约束，因此有可能要进行调整。

#define RED        0    // 红色节点#define BLACK    1    // 黑色节点typedef int Type;// 红黑树的节点typedef struct RBTreeNode{    unsigned char color;        // 颜色(RED 或 BLACK)    Type   key;                    // 关键字(键值)    struct RBTreeNode *left;    // 左孩子    struct RBTreeNode *right;    // 右孩子    struct RBTreeNode *parent;    // 父结点}Node, *RBTree;// 红黑树的根typedef struct rb_root{    Node *node;}RBRoot;

*/static void rbtree_left_rotate(RBRoot *root, Node *x){    // 设置x的右孩子为y    Node *y = x->right;    // 将 “y的左孩子” 设为 “x的右孩子”；    // 如果y的左孩子非空，将 “x” 设为 “y的左孩子的父亲”    x->right = y->left;    if (y->left != NULL)        y->left->parent = x;    // 将 “x的父亲” 设为 “y的父亲”    y->parent = x->parent;    if (x->parent == NULL)    {        //tree = y;            // 如果 “x的父亲” 是空节点，则将y设为根节点        root->node = y;            // 如果 “x的父亲” 是空节点，则将y设为根节点    }    else    {        if (x->parent->left == x)            x->parent->left = y;    // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”        else            x->parent->right = y;    // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”    }        // 将 “x” 设为 “y的左孩子”    y->left = x;    // 将 “x的父节点” 设为 “y”    x->parent = y;}

*/static void rbtree_right_rotate(RBRoot *root, Node *y){    // 设置x是当前节点的左孩子。    Node *x = y->left;    // 将 “x的右孩子” 设为 “y的左孩子”；    // 如果"x的右孩子"不为空的话，将 “y” 设为 “x的右孩子的父亲”    y->left = x->right;    if (x->right != NULL)        x->right->parent = y;    // 将 “y的父亲” 设为 “x的父亲”    x->parent = y->parent;    if (y->parent == NULL)     {        //tree = x;            // 如果 “y的父亲” 是空节点，则将x设为根节点        root->node = x;            // 如果 “y的父亲” 是空节点，则将x设为根节点    }    else    {        if (y == y->parent->right)            y->parent->right = x;    // 如果 y是它父节点的右孩子，则将x设为“y的父节点的右孩子”        else            y->parent->left = x;    // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子”    }    // 将 “y” 设为 “x的右孩子”    x->right = y;    // 将 “y的父节点” 设为 “x”    y->parent = x;}

*/static void rbtree_insert(RBRoot *root, Node *node){    Node *y = NULL;    Node *x = root->node;    // 1. 将红黑树当作一颗二叉查找树，将节点添加到二叉查找树中。    while (x != NULL)    {        y = x;        if (node->key < x->key)            x = x->left;        else            x = x->right;    }    rb_parent(node) = y;    if (y != NULL)    {        if (node->key < y->key)            y->left = node;                // 情况2：若“node所包含的值” < “y所包含的值”，则将node设为“y的左孩子”        else            y->right = node;            // 情况3：(“node所包含的值” >= “y所包含的值”)将node设为“y的右孩子”     }    else    {        root->node = node;                // 情况1：若y是空节点，则将node设为根    }    // 2. 设置节点的颜色为红色    node->color = RED;    // 3. 将它重新修正为一颗二叉查找树    rbtree_insert_fixup(root, node);}

static void rbtree_delete_fixup(RBRoot *root, Node *node, Node *parent){    Node *other;    while ((!node || rb_is_black(node)) && node != root->node)    {        if (parent->left == node)        {            other = parent->right;            if (rb_is_red(other))            {                // Case 1: x的兄弟w是红色的                  rb_set_black(other);                rb_set_red(parent);                rbtree_left_rotate(root, parent);                other = parent->right;            }            if ((!other->left || rb_is_black(other->left)) &&                (!other->right || rb_is_black(other->right)))            {                // Case 2: x的兄弟w是黑色，且w的俩个孩子也都是黑色的                  rb_set_red(other);                node = parent;                parent = rb_parent(node);            }            else            {                if (!other->right || rb_is_black(other->right))                {                    // Case 3: x的兄弟w是黑色的，并且w的左孩子是红色，右孩子为黑色。                      rb_set_black(other->left);                    rb_set_red(other);                    rbtree_right_rotate(root, other);                    other = parent->right;                }                // Case 4: x的兄弟w是黑色的；并且w的右孩子是红色的，左孩子任意颜色。                rb_set_color(other, rb_color(parent));                rb_set_black(parent);                rb_set_black(other->right);                rbtree_left_rotate(root, parent);                node = root->node;                break;            }        }        else        {            other = parent->left;            if (rb_is_red(other))            {                // Case 1: x的兄弟w是红色的                  rb_set_black(other);                rb_set_red(parent);                rbtree_right_rotate(root, parent);                other = parent->left;            }            if ((!other->left || rb_is_black(other->left)) &&                (!other->right || rb_is_black(other->right)))            {                // Case 2: x的兄弟w是黑色，且w的俩个孩子也都是黑色的                  rb_set_red(other);                node = parent;                parent = rb_parent(node);            }            else            {                if (!other->left || rb_is_black(other->left))                {                    // Case 3: x的兄弟w是黑色的，并且w的左孩子是红色，右孩子为黑色。                      rb_set_black(other->right);                    rb_set_red(other);                    rbtree_left_rotate(root, other);                    other = parent->left;                }                // Case 4: x的兄弟w是黑色的；并且w的右孩子是红色的，左孩子任意颜色。                rb_set_color(other, rb_color(parent));                rb_set_black(parent);                rb_set_black(other->left);                rbtree_right_rotate(root, parent);                node = root->node;                break;            }        }    }    if (node)        rb_set_black(node);}